Disziplin Wurzel

Schnelles Wurzelziehen

Versuch doch mal folgende Aufgabe im Kopf zu berechnen:
Quadratwurzel aus 75076 = ?

Das ziehen einer Wurzel ist eine komplexe Rechenaufgabe. Das können die wenigsten Menschen ohne einen Taschenrechner lösen. Die Kopfrechenmeister machen das sogar im Kopf.

Wenn jemand von Wurzel ziehen spricht ist üblicherweise die Quadratwurzel gemeint. Also die zweite Wurzel wird Quadratwurzel genannt. Eine Wurzel ist eine umgedrehte Potenz. Wenn wir die 2. Potenz von 9 nehmen ist das 9 hoch 2 oder auch 9*9 = 81. Wenn wir dann die Wurzel von 81 ziehen wollen ist das wieder die 9. Das ist die 2. Potenz oder die Quadratwurzel. Als Übersicht hier de Potenzen von 1-32.

Wenn du dir die Ergebnisse ansiehst kannst du feststellen, daß die Potenz von 1 und 9 immer mit 1 Endet. Die Potenz von 2 & 8 immer auf 4, die Potenz von 3 & 7 immer auf 9 und die Potenz von 4 & 6 immer auf 6 Endet. Die Potenz von 5 auf 5 und die vom x0 auf 0. Das ist für das weiter vorgehen wichtig.

In der Schule haben wir Wurzel ziehen so gelernt:

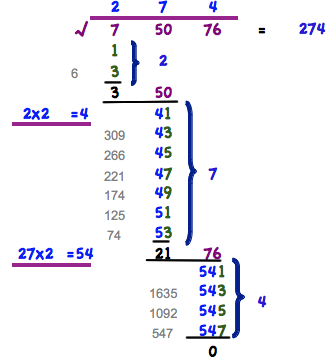
• 1. Zahl nach links in Zweiergruppen aufteilen
• 2. Nun von der linken Gruppe ungerade Zahlen abziehen. Mit 1 beginnen, solange bis noch ein positiver Rest da ist! Also 7-1=6, 6-3=3, 3-5= - 2 geht nicht mehr..
• 3. Die Anzahl der ungeraden Zahlen Zählen. Das ist die 1. Ziffer der Lösung (2).
• 4. Zu dem Rest (3) die nächste 2er-Gruppe (50) hinzufügen. Das ergibt die Zahl 350.
• 5. Das bisherige Ergebnis mit 2 multiplizieren (2x2=4). Das ist die neue Basis an die wir die ungeraden Zahlen anhängen (4x) und von dem Wert (350) abziehen
• 6. Wie bei 2 beschrieben vorgehen. 350-41=309, 309-43=266, 266-45…..
• 7. Wie bei 3.- 5. beschrieben vorgehen. 3. Anzahl ungerader Zahlen (7), 2. Ziffer der Lösung. 4. Nächste 2er-Gruppe dazu (2176), 5. Ergebnis mit mal 2 (27x2 = 54)
• 8. Wie ab 4. beschrieben vorgehen. Rest (21) und nächster 2-er Block (76), ergibt (2176). 2176-541=1635, 1635-543=1092,…

Die Schritte ab 5. kannst du solange wiederholen, bis das Ergebnis ausreichend genau oder der Rest 0 ist.

Ein andere Weg um eine Quadratzahl zu lösen:

Hierzu benötigst du die Potenzen vom Anfang des Artikels.

Unserem Beispiel Wurzel aus 75076

Wir teilen die 75076 in 2 Blöcke. 750 & 76

Also endet die Potenz auf 76. Daraus ergibt Potenz von 4 & 6, weil diese immer auf 6 Enden

Nun suche wir die größte mögliche Potenz die die 750 nicht übersteigt. Das ist die 27. Denn 27x27=729

Also kann die Lösung nur 27 4 oder 27 6 sein.

Wir bedienen uns einen Trick und nehmen die Potenz die dazwischen liegt und mit 5 endet. Also die Potenz aus 275.

Potenzen mit fünf sind relativ leicht zu berechnen. Hierzu teilen wir die 275 in 27 & 5. Dann nehmen wir die 5x5 = 25 und die 27 x 27+1 = 27x28. Das ist dann die Potenz aus 27= 729+27= 756. Nun die beiden Ergebnisse verbinden - 75625

Nun die Prüfung liegt die gesuchte Wurzel (75076) unter der Potenz von xx5 (75625) dann ist es die Niedrige der beiden möglichen Potenzen, liegt sie da drüber ist es die andre

Also die gesuchte liegt unter der 5er Potenz also ist die 274 die richtige.

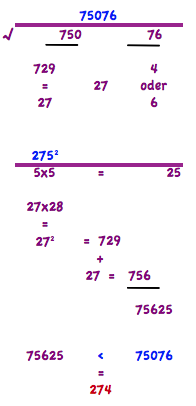
Nehmen wir zur Verdeutlichung noch ein anders Beispiel. Gesucht wird die Wurzel aus 12769. Das ergibt in 2 Böcke 127 & 69. Also Endet auf 9. Mögliche Potenzen mit 3 oder 9. Die größte Potenz die 127 nicht übersteigt ist die 11. Also mögliche Kandidaten 11 3 & 11 9. Nun die Potenz von 115. 11x11 = 121.+ 11= 132. 132 & 25= 13225. Das ist wieder über der gesuchten 12769, also die unter der beiden Kandidaten. Ergibt Wurzel 12769 = 113.

So geht das ganze im Kopf:

Da ich keine vernünftige Anleitung zum ziehen einer Quadradwurzel gefunden habe warte ich auf eine Anleitung von einem Kopfrechensportler.

Anleitung: Wurzel ziehen - Quadratwurzel berechnen

Hier geht es darum die Quadratwurzel aus einer fünfstelligen Zahl, im Kopf, zu ziehen. Mit etwas Übung wirst du das sicher schaffen.

Je besser du wirst, um so höher wird dein Level.

Hier die Leveleinteilung: