Um diesen Inhalt anzuzeigen muss eine Verbindung zu Youtube / Google hergestellt werden. Dabei werden von Ihrem Browser eventuell persönliche Daten übertragen und ausgewertet. Wollen Sie dennoch fortfahren?
Multiplicaciones rápidas
Intenta calcular tarea siguiente en la mente:
319 x 546 = ?
Multiplicar con números de una cifra es relativamente fácil. Ya aprendimos en la escuela las tablas de multiplicar y lo podemos hacer de cabeza. Multiplicar con números pequeños de dos cifras también funciona, más o menos desde el 1x1 al 20x20. Y hasta ahí llegamos con los cálculos de cabeza normalmente y ya empezamos a multiplicar con papel y lápiz.
En la escuela aprendimos a multiplicar de forma escrita así:
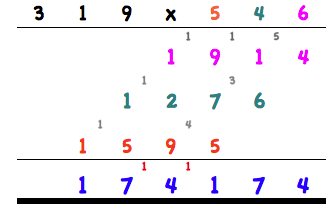
Empezamos por la derecha y multiplicamos las cifras 6x9=54. El 4 lo escribimos en la primera fila y memorizamos el 5. Entonces 6x1=6. 6 más el 5 que habíamos memorizado =11. Un 1 abajo a la izquierda del 4. Entonces 6x3=18 más el 1 que habíamos memorizado =19. Hacemos lo mismo con el 4 de 546. Así que 4x9=36. El 6 debajo del 4 en una segunda fila y nos llevamos 3. Y así sicesivamente. Demasiados pasos para que uno pueda hacerlos de cabeza.
¿Cómo se multiplica de cabeza?
El método de los deportistas de la memoria es el llamado la multiplicación védica. Este método de multiplicación viene de la India y facilita considerablemente los cálculos de cabeza. Con este ejemplo os quiero presentar el método.
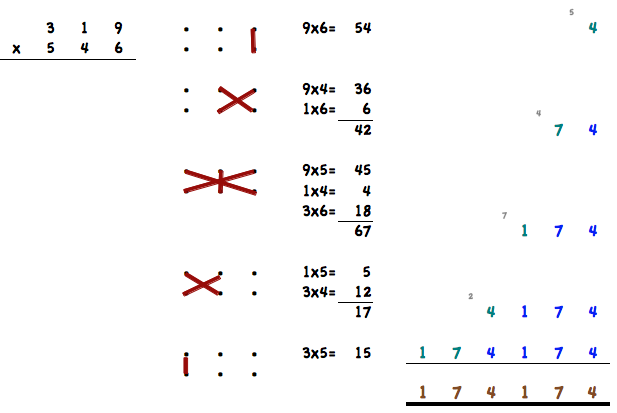
Este método se llama también método de la cruz. Mediante el gráfico podrás ver por qué. Primero tomamos las dos cifras de la derecha. 9x6=5. El 4 ya lo puedes escribir como solución abajo. Nos llevamos el 5. El siguiente paso es tomar las últimas dos cifras. 9x4=36 y 1x6=6. Juntas dan 42 + el 5 que nos habíamos llevado =47. El 7 ya lo puedes escribir abajo como solución y llevarte el 4. El tercer paso es tomar todas las cifras y entrecruzarlas. 9x5=45, 1x4=4, 3x6=18. Todas juntas dan 67 + el 4 que nos llevábamos =71. El 1 como solución y nos llevamos el 7. El cuarto paso es entrecruzar las dos cifras de la izquierda. 1x5=5, 3x4=12 que da 17 más los 7 que nos llevábamos =24. El 4 lo apuntamos y nos llevamos 2. El último paso es multiplicar las dos cifras de la derecha. 3x5=15 más 2 que nos llevábamos nos da 17. Por supuesto anotar esto también. La gran ventaja del método es que puedes anotar las soluciones directamente abajo de derecha a izquierda. Así te ahorras todas esas anotaciones intermedias que tenía el método de la multiplicación escrita.
En los campeonatos de multiplicación de cabeza se multiplican números de dos cifras entre sí.

Como puedes ver es el mismo principio que en el de la multiplicación 3x3. De derecha a izquierda y entrecruzado. Para practicar te recomiendo primero 2x2 cifras y luego con 3x3. Cuando hayas comprendido el principio, podrás calcular hasta 5x5 de cabeza. Aquí también depende de la práctica, pero merece la pena. Al calcular de cabeza se usan los dos hemisferios cerebrales a la vez, es un entrenamiento cerebral excelente.
Instrucciones: Multiplicación
Hier geht es darum so schnell wie möglich zwei dreistellige Zahlen im Kopf zu mutiplizieren. Das möglichst schnell und Fehlerfrei. Mit etwas Übung wirst du das sicher schaffen.
En primer lugar, la información llega a nuestra ultra-memoria a corto plazo, una especie de tampón en el que toda la información que llega a nuestros sentidos se almacenan corto. El periodo en el que se almacenan la información es de aproximadamente 0,1 a 2 segundos. Esto ha sido estudiado en pruebas diferentes y descubierto.
| 832 | |
| x | 678 |
El matemático alemán, físico y médico, Johann Andreas von Segner, trató en 1740 con la memoria de ultra-corto plazo. En los primeros estudios de la memoria de ultra-corto plazo, se dice que ha llevado a cabo un experimento en 1740 en la que dejó en un cuarto oscuro girar un carbón encendido en una rueda. La rueda tomó velocidad. Los sujetos deberán decir cuando ya no pueden realizar un solo carbón sinó un círculo cerrado de la luz. Con el uso de esto, Segner fijó el momento de transición determinado, el tiempo de almacenamiento de la memoria de ultra-corto plazo. Este fue de 0,1 a 0,5 segundos. El cerebro sólo puede percibir un círculo, si es lo suficientemente largo recordar donde estaba antes este punto.
Memoria a largo plazo es, ya que el psicólogo canadiense Endel Tulving 1972 publicó sus estudios, dividido en dos grupos principales: la memoria declarativa (también llamada memoria de conocimiento) y la memoria procedimental (también llamado comportamiento de la memoria).
La memoria declarativa / memoria de conocimiento
| Level | <=5 min | La memoria declarativa a su vez tiene dos subespecies: la memoria episódica (memoria o personal) y la memoria semántica (o memoria general). | × 5 Stellen | La memoria declarativa a su vez tiene dos subespecies: la memoria episódica (memoria o personal) y la memoria semántica (o memoria general). | × 8 Stellen | La memoria declarativa a su vez tiene dos subespecies: la memoria episódica (memoria o personal) y la memoria semántica (o memoria general). | <=5 min | La memoria declarativa a su vez tiene dos subespecies: la memoria episódica (memoria o personal) y la memoria semántica (o memoria general). |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 3 | 3 | 0 | 3 | 0 | 3 | 0 | 3 | 0 |
| 4 | 4 | 0 | 6 | 0 | 4 | 0 | 4 | 0 |
| 5 | 5 | 0 | 9 | 0 | 5 | 0 | 5 | 0 |
| 6 | 6 | 0 | 12 | 0 | 6 | 0 | 6 | 0 |
| 7 | 6 | 1 | 12 | 3 | 6 | 1 | 6 | 1 |
| 8 | 7 | 1 | 15 | 3 | 7 | 1 | 7 | 1 |
| 9 | 8 | 1 | 18 | 3 | 8 | 1 | 8 | 2 |
| 10 | 9 | 1 | 21 | 3 | 9 | 1 | 10 | 2 |
| 11 | 10 | 1 | 24 | 3 | 10 | 1 | 12 | 2 |
| 12 | 11 | 1 | 27 | 3 | 11 | 1 | 14 | 2 |
| 13 | 12 | 1 | 30 | 3 | 12 | 1 | 16 | 2 |
| 14 | 12 | 2 | 30 | 6 | 12 | 2 | 16 | 4 |
| 15 | 13 | 2 | 33 | 6 | 13 | 2 | 18 | 4 |
| 16 | 14 | 2 | 36 | 6 | 14 | 2 | 20 | 4 |
| 17 | 15 | 2 | 39 | 6 | 15 | 2 | 22 | 4 |
| 18 | 16 | 2 | 42 | 6 | 16 | 2 | 24 | 4 |
| 19 | 17 | 2 | 45 | 6 | 17 | 2 | 26 | 4 |
| 20 | 20 | 0 | 54 | 0 | 20 | 0 | 32 | 0 |
 Menü
Menü
